Three Sided Dice

(Color Version of the Three Sided Die Problem and Solution)

Maximum Entropy Solution to the Three Sided Die (Chapter 4)

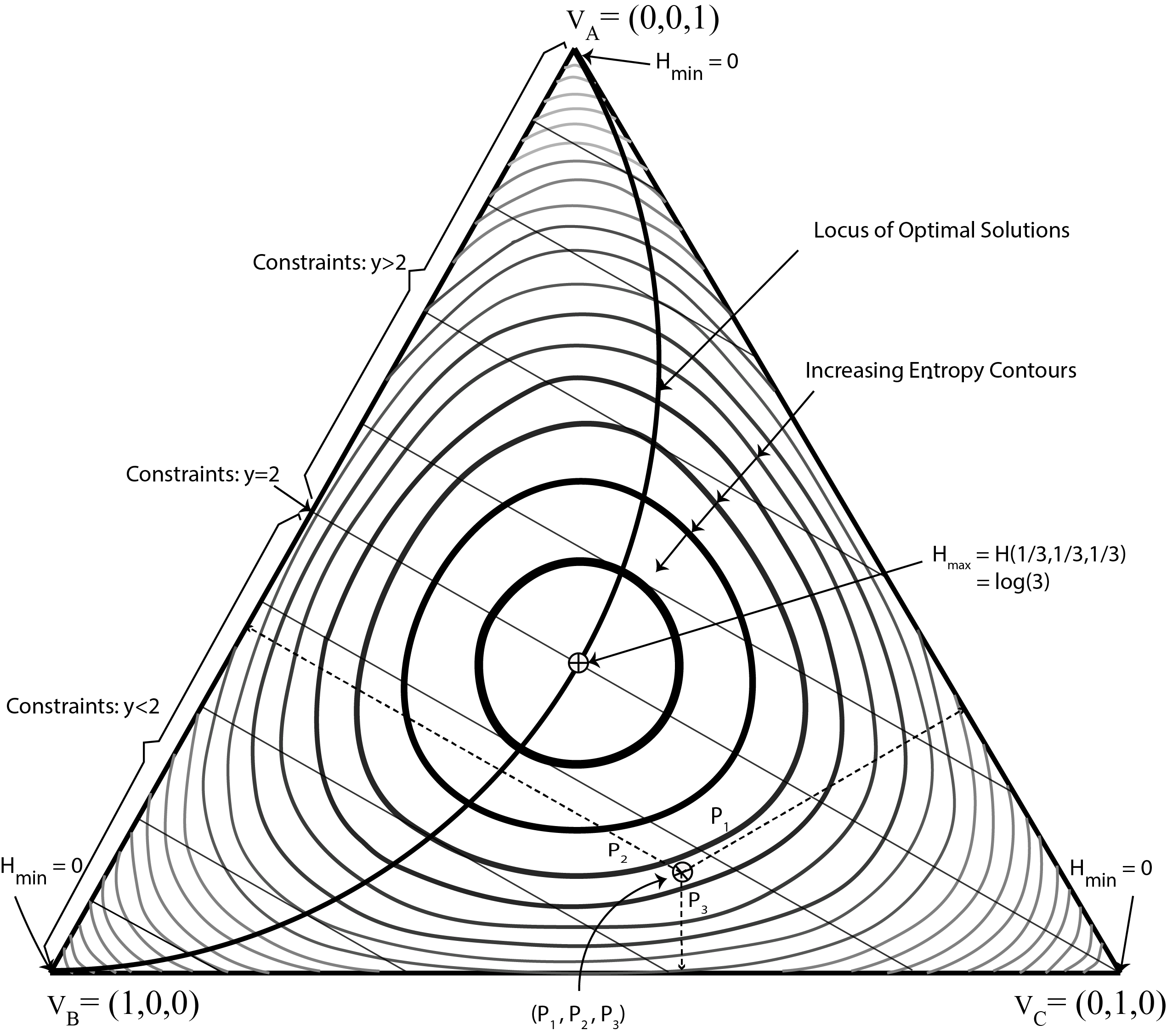
The Problem: Consider a discrete random variable with three possible values: 1, 2 and 3. We call it a three-sided die. We know the mean value after playing the die for many games. We call this mean y. We want to infer the probability of the next outcome.

This example presents the solution for different values of y. It is a simplex representation of the maximum entropy solution for a discrete probability distribution defined over three possible events. Here it represents a three-sided die with values of 1, 2 and 3. The vertices V_B , V_C , and V_A are the extreme distributions (1, 0, 0) , (0, 1, 0), and (0, 0, 1) respectively for 1, 2 and 3.

Every point inside the triangle is a distribution where the values correspond to the distances from the sides V_A V_C , V_B V_A and V_B V_C respectively, and normalized such that Σp_k = 1. The midpoint is the uniform distribution (1/3, 1/3, 1/3). It has maximal entropy of log(3). The contours connect distributions of equal entropy. The straight lines are the linear constraint set for different values of y for. Contours far away from the center have lower entropy with an entropy of exactly zero at each one of the three vertices.